今回も前回に続きExcelを使った野球の投球軌道シミュレーションをしていこうと思います。

↓ 毎度お世話になっている参考サイトさん
前回までの実装内容
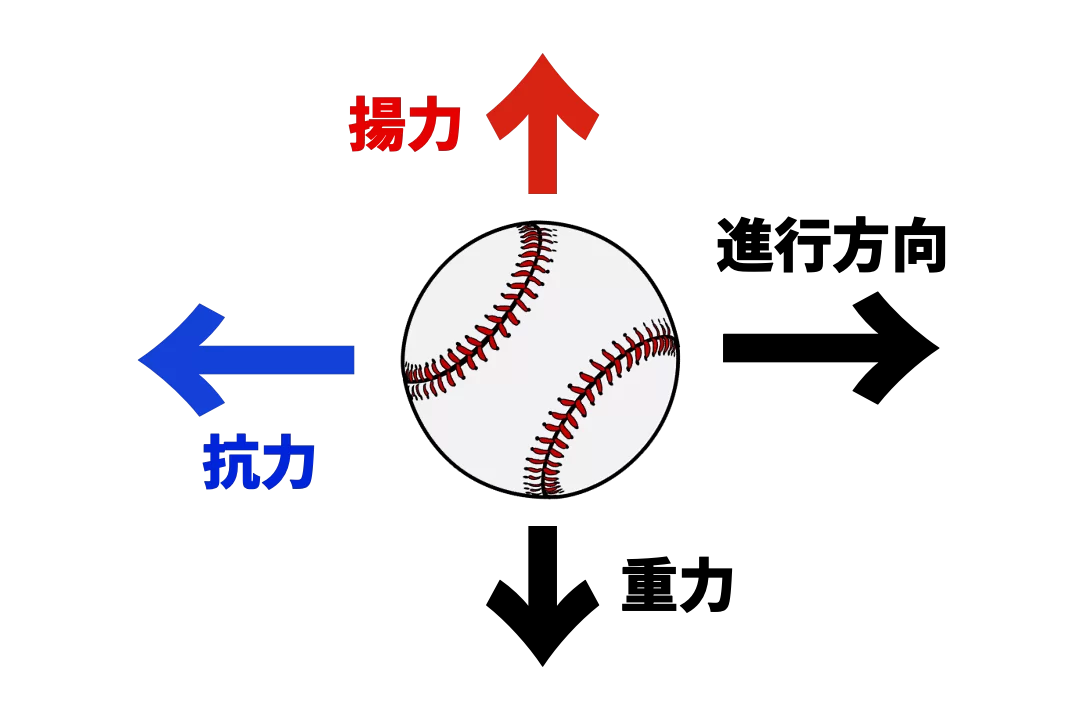
前回は投球にかかる力や物理の基本的な話を勉強してきました。

そして、Excelを使い力のかかる向きを進行方向のみで
空気や重力のような現実世界の物理を全て無視して考えました。

今回は前回の進行方向への「等速直線運動」に加え、上記のように重力を実装しようと思います。
第3回 軌道シミュレータver.2 -自由落下運動-
今回も参考記事に従って作っていきます。
今回参考にする記事 第3回 軌道シミュレータver.2 -自由落下運動-
はじめに

今回の「進行方向の力」と「重力」のみを考えるような動きを「自由落下運動」と言います。
これは物理初心者の私でも知っていました!笑
確か、高校物理のほとんどの問題が空気抵抗を考慮しない「自由落下運動」でしたね。
重力は、質量[kg]×重力加速度[m/s2]で求められます。
参考記事では、重力加速度が高校物理同様 9.8 としていますが
今回私はできる限り正確にシミュレーションしたいので重力加速度は、9.80665 とします。
余談 ガリレオによるピサの斜塔実験
余談ですが、物の落ちる速度の話を調べてみると面白い物理法則がありました。
それが「落体の法則」です。
これは空気の真空中での落下、すなわち自由落下において速さと重さは関係ないというものです。
現実世界で考えると重いものが早く落下し、軽いものは遅く落下するというのが当たり前ですよね。
ただ、自由落下においては質量関係なく全て同時に落下します。
空気があると落下速度が質量によって異なるのは、空気抵抗が関係しているからです。
計算方法について
重力は -0.5×g×t2 です。
この式は高校物理で習いましたね。
私も今だに覚えていました。
計算式は以下のようです。
x = x0 + v0 × cosθ × cosφ × t
y = y0 + v0 × cosθ × sinφ × t
z = z0 + v0 × sinθ × t – 0.5 × g × t2
x0, y0, z0:リリース位置 v0:リリース時の球速
θ:上向きリリース角度 φ:横向きリリース角度
t:リリース後経過時間 g:重力加速度
今回の重力は下向き、すなわちZ軸方向にしか力がかからないので
Z座標の計算式以外のX座標とY座標の計算式は前回そのままです。
実際にExcelでシミュレーションしてみる
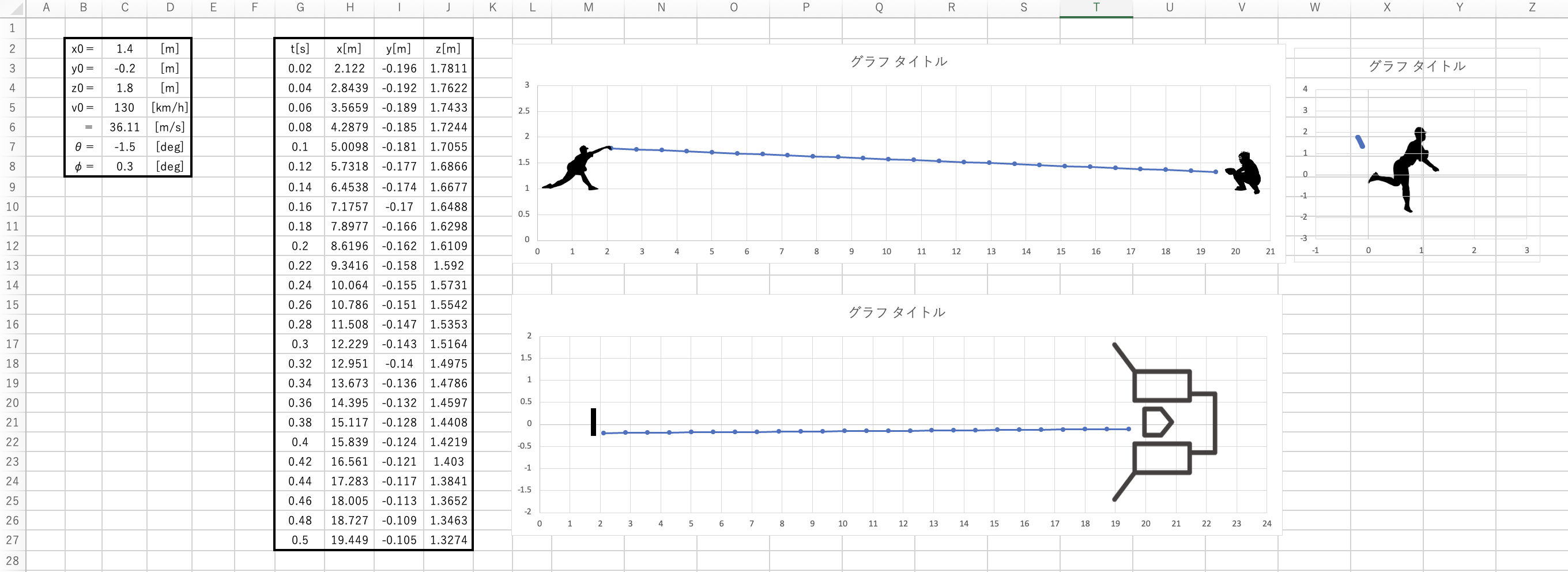
前回はデータが、ムチャクチャでボールが地面にのめり込んだり
サイドスロー並みの横移動だったので、データをしっかり修正しました。
プロ野球の人のラプソードのデータを参考に修正したのである程度は正確だと思います。
あと、前回のプロット数が少なすぎて見にくかったので、参考記事と同様の 0.02s 間隔にしました。
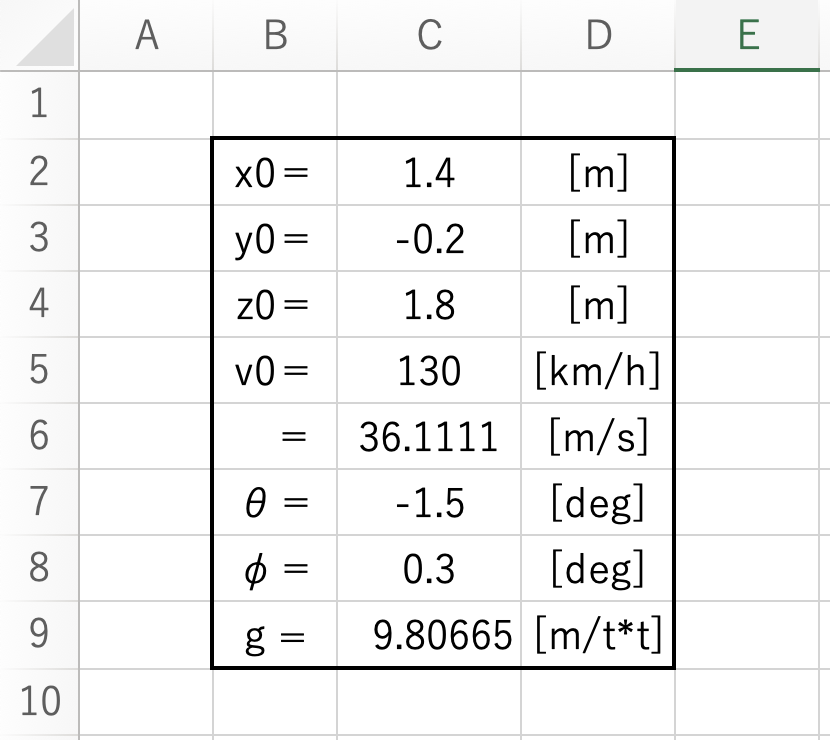
重力加速度のgを追加しました。
今回の定数に関する変更点はこれだけです。
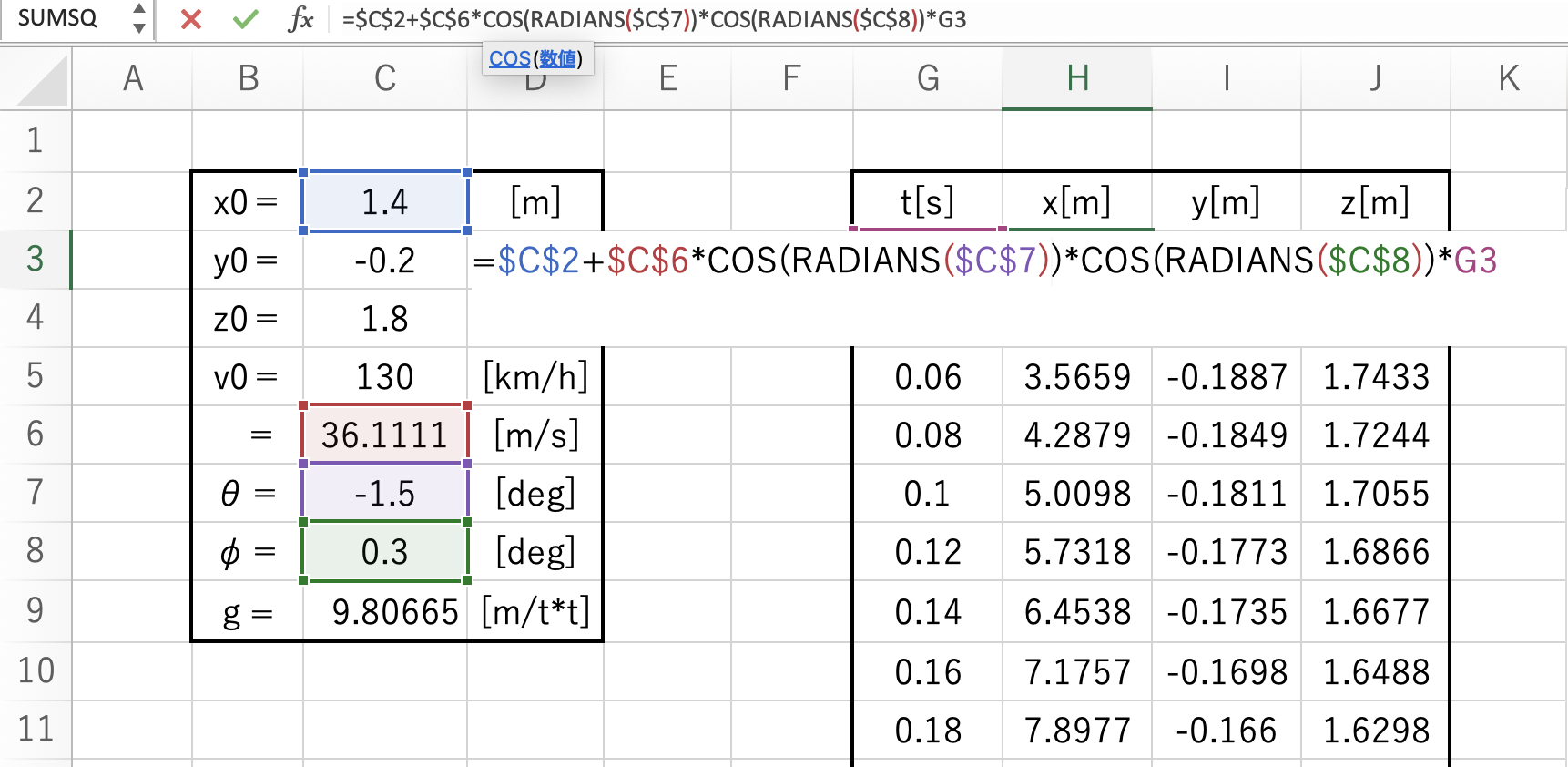
先ほども言った通り、X座標は前回そのままです。
=$C$2+$C$6COS(RADIANS($C$7))COS(RADIANS($C$8))*G3

Y座標は前回そのままです。
=$C$3+$C$6COS(RADIANS($C$7))SIN(RADIANS($C$8))*G3
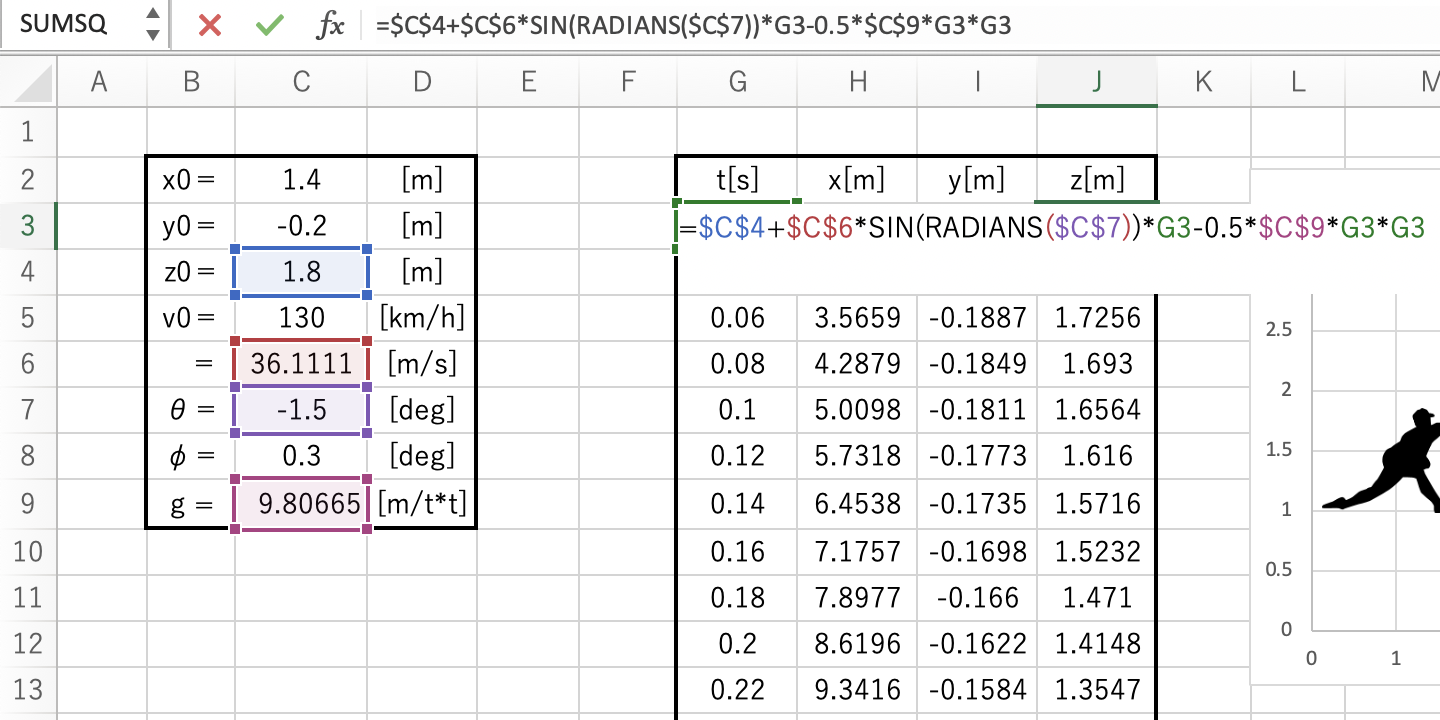
Z座標は前回の計算式から重力 – 0.5 × g × t2 を引くだけでOKです!
=$C$4+$C$6SIN(RADIANS($C$7))G3-0.5$C$9G3*G3
重力加速度も定数なので F4 か $ で固定してください。
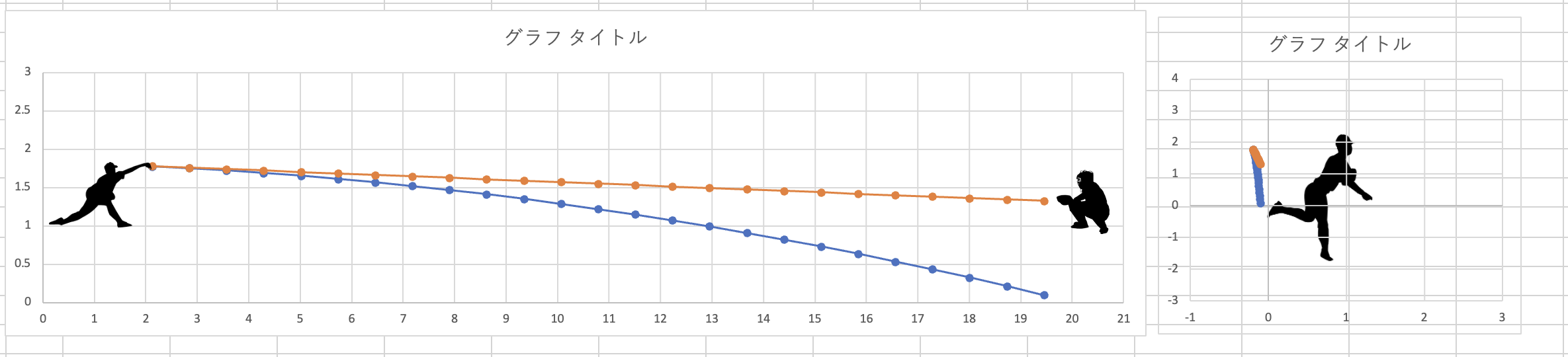
できました!
今回は前回と比較できるように色分けして表示してみました。
オレンジ色のグラフが前回の空気・重力を考えない投球軌道です。
青色のグラフが今回の自由落下運動の投球軌道です。
しっかり落ちていますね。
今回はまだ続きます。
第5回 軌道シミュレータver.3.0 -抗力-
次は抗力という、ボールの進行方向に対して逆にかかる力を計算して再現していきます。
はじめに

これで4方向のうち3つ目ですね。
この抗力は主に空気抵抗というやつですね。
今回は抗力のみなのでX軸方向の空気抵抗です。
計算方法について
空気抵抗Dの公式は以下の通りです。
D = CD × ( 0.5 × ρ × v2 ) × A
速度以外は定数です。
ということは空気抵抗Dは速度vに依存するということです。
また、抗力はX軸方向なので今回変更する計算式はX座標のみです。
実際にExcelでシミュレーションしてみる
X座標の計算式について理解していきます。
計算式自体は参考サイトにあるので、あとは理解していくだけです(笑)
空気抵抗は先ほどの式をそのまま使い
D = CD × ( 0.5 × ρ × v2 ) × A
加速度の求め方は、高校物理で覚えた運動方程式 m(質量)×a(加速度)=F(加えた力)を変形して
a(加速度)=F(加えた力)÷ m(質量)で求められます。
a = -F / m
すなわち、今回の計算における加速度は D(空気抵抗) ÷ m(質量)で求められます。
速度は、速度の公式より
dx/dt = vx
これらの式から、
加速度
a = d2x/dt2 = -CD × ( 0.5 × ρ × (dx/dt)2 ) × A / m
速度
dx/dt = ∮(d2x/dt2)dt
位置
x = ∮(dx/dt)dt
それぞれ、応用の物理で勉強した内容ですね。
若干記憶にありましたが、これはもうかなりガチ理系ですね、
改めて物理の微分と積分の関係性を調べ直しました笑
t = 0 のとき
速度
dx/dt = v0 × cosθ × cosφ
位置
x = x0
Y座標とZ座標の計算式は以下のようにこれまで同様です。
y = y0 + v0 × cosθ × sinφ × t
z = z0 + v0 × sinθ × t – 0.5 × g × t2
x0, y0, z0:リリース位置 v0:リリース時の球速
θ:上向きリリース角度 φ:横向きリリース角度
t:リリース後経過時間 g:重力加速度
実際にExcelでシミュレーションしてみる
では実際にExcelに入力していきます。
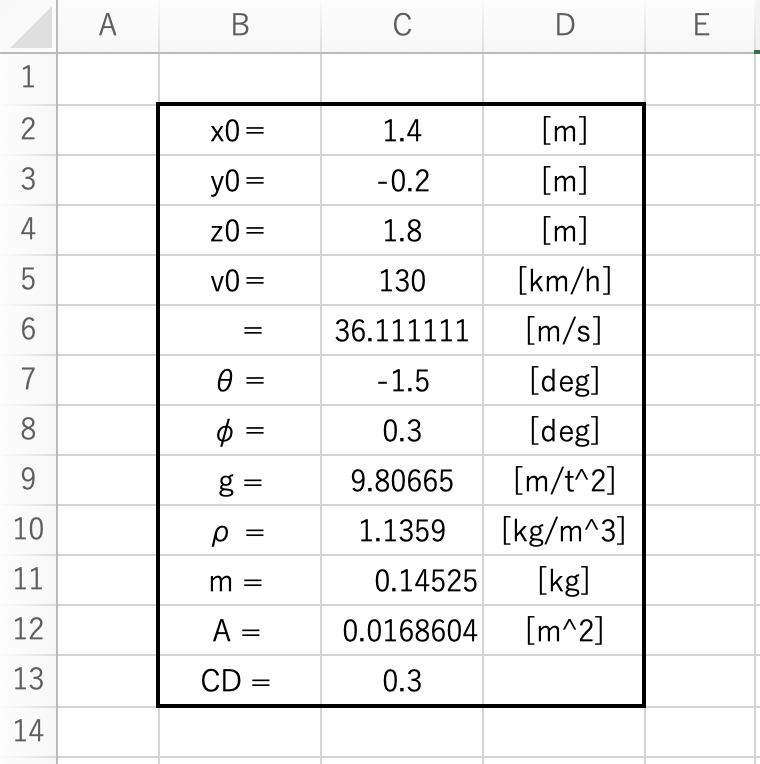
上記のように定数をまず設定しました。
これまでに引き続き、今回は ρ, m, A, CDを定数として新たに設定します。
ρ:空気密度は状態方程式より求められます。
状態方程式より気温と気圧が分かれば ρ:空気密度を求めることができます。
私はこのサイトを使って計算しました。
気温と気圧は、私の住んでいる愛知県の春日井市の昼時の平均情報(8月)を使いました。
m:質量は硬式野球ボールの規定に則って 0.1417~0.1488kg の平均である 0.14525kg を使用しました。
A:断面積は硬式野球ボールの規定に則って
直径 72.93~74.84mm の平均を求め、半径に変換して、π × 半径 × 半径で求めました。
CD:抗力係数は求めることが、かなり難しく(実際に実験や計算をしないといけない)
また球種によっても変化しますが、野球ボールに関する先行研究をいくつか調べてみたところ
直球系の球種に関しては、どれも大体 0.3 付近でした。
なので、今回は 0.3 として計算します。

次に t となる描画間隔ですが
参考記事によると、描画間隔を短くすればするほど正確なシミュレーションができるということなので
0.2s から 0.1s に変更しました。
ちょいちょい理解していないところがあってすみません笑
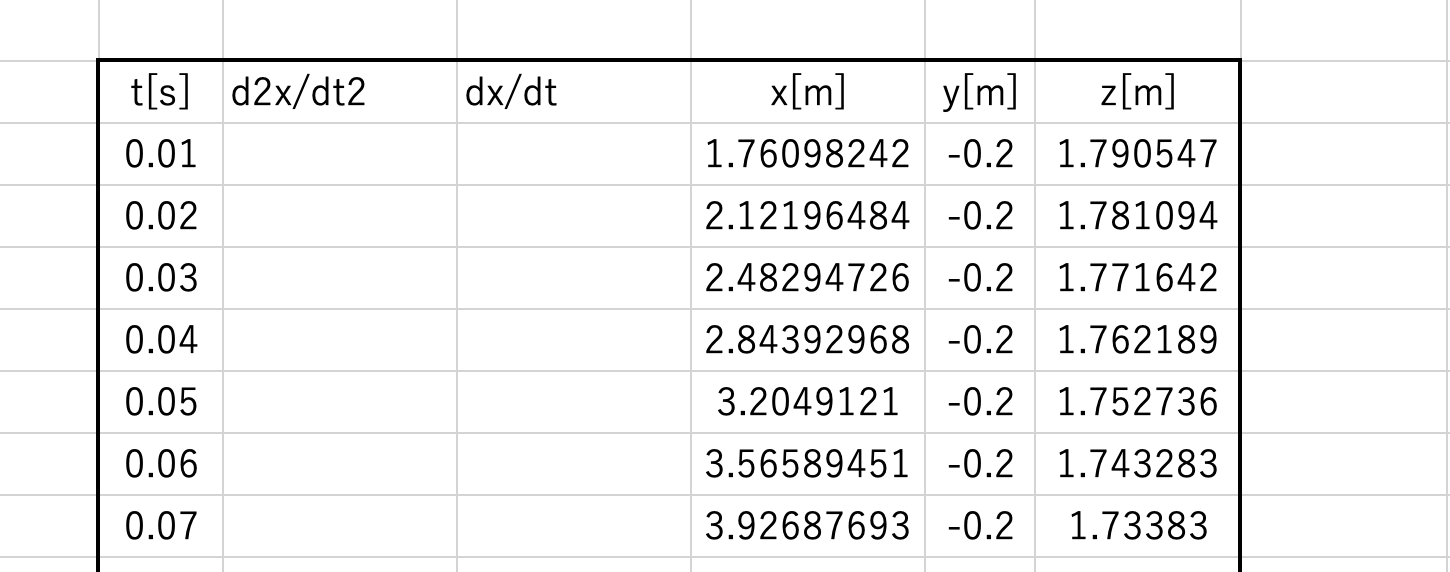
加速度と速度の欄を追加しました。
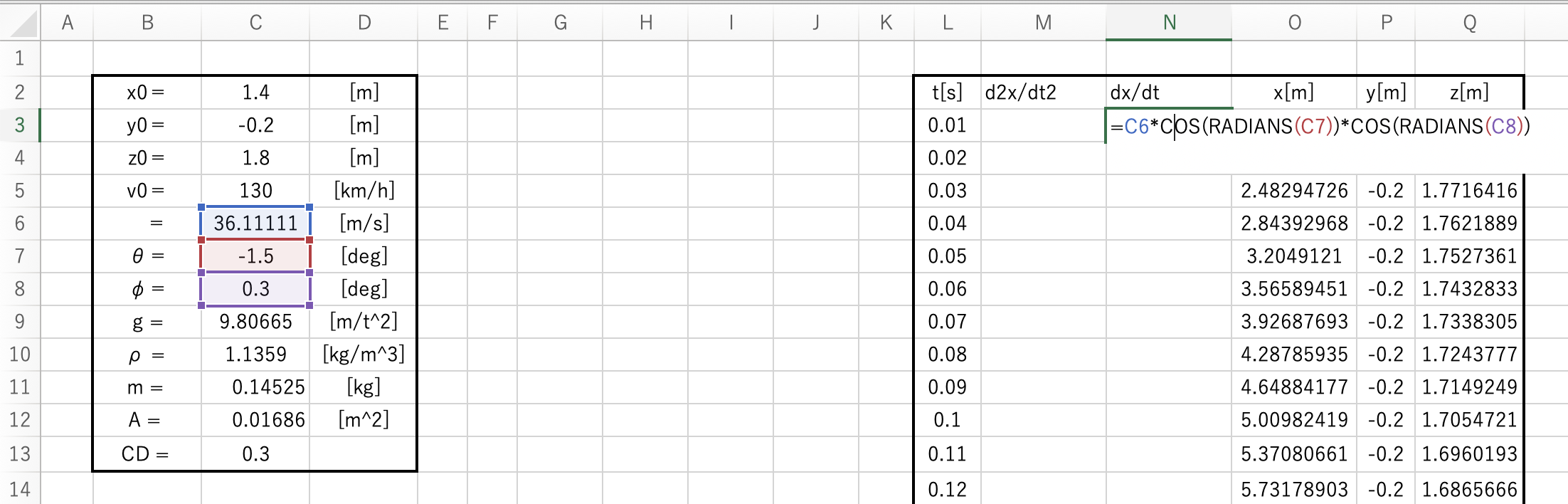
先ほどの t = 0 のときの速度計算式より t = 0 のときの速度を入力。
=C6COS(RADIANS(C7))COS(RADIANS(C8))
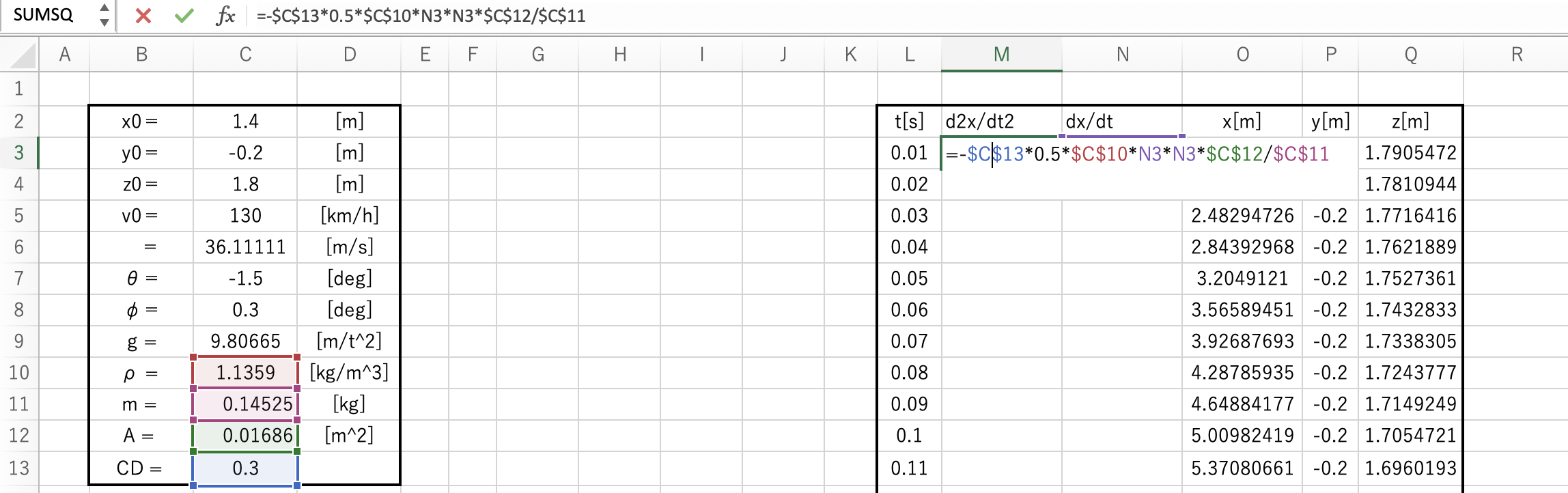
次に加速度を先ほどの計算式を入力していきます。
=-$C$130.5$C$10N3N3*$C$12/$C$11

また、今度は t = 0ではないときの通常の速度を求める計算式を入力していきます。
ただ、速度を求めるには積分をするのですが、積分を分解して普通に計算していきます。

あっすみません、t が 0 からじゃなかったので修正しました。
0.01 だったセルを 0 に変えるだけで全部自動で値が変わるのでExcelは便利ですね ^^;
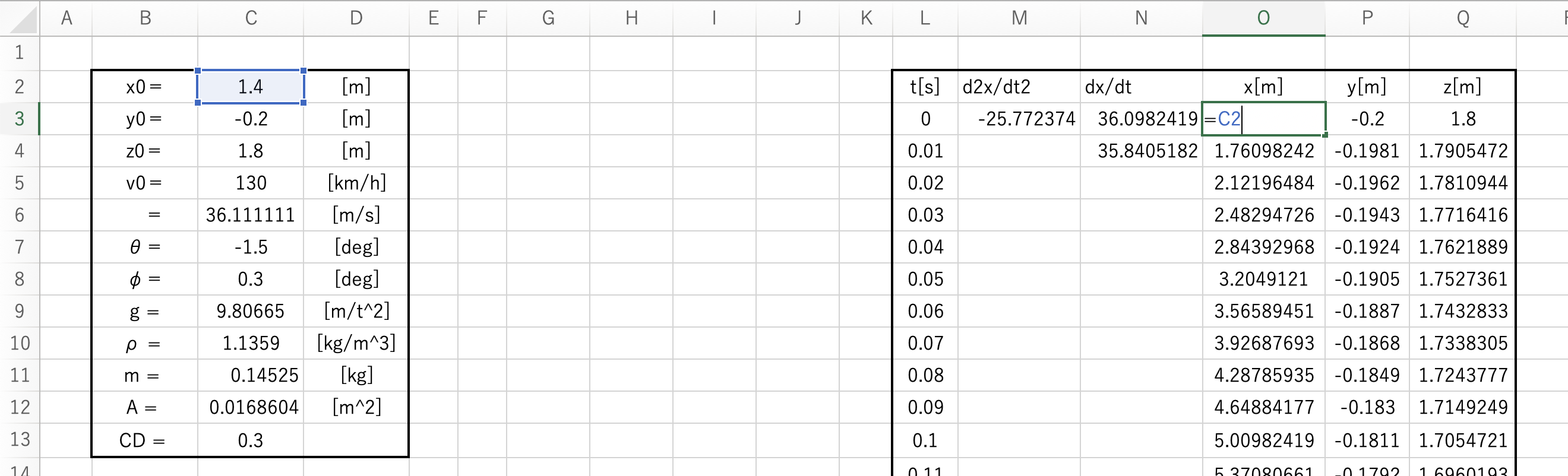
t = 0 のときの位置の計算式を入力します。
といってもリリースポイントの初期値そのまま渡すだけですが笑
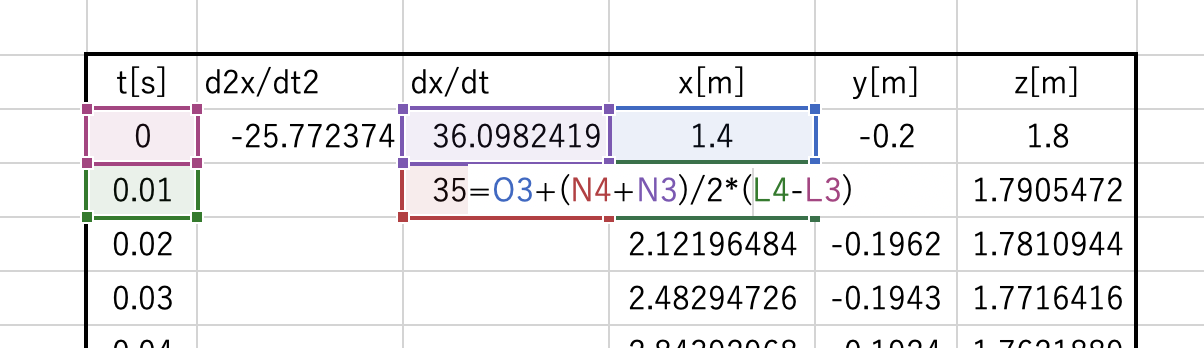
また、今度は t = 0ではないときの通常の速度を求める計算式を入力していきます。
ただ、こちらも速度同様、位置を求めるには積分をするのですが、積分を分解して普通に計算していきます。

Y座標はこれまでと同様です。
=$C$3+$C$6COS(RADIANS($C$7))SIN(RADIANS($C$8))*G3

Z座標もこれまでと同様です。
=$C$4+$C$6SIN(RADIANS($C$7))G3-0.5$C$9G3*G3
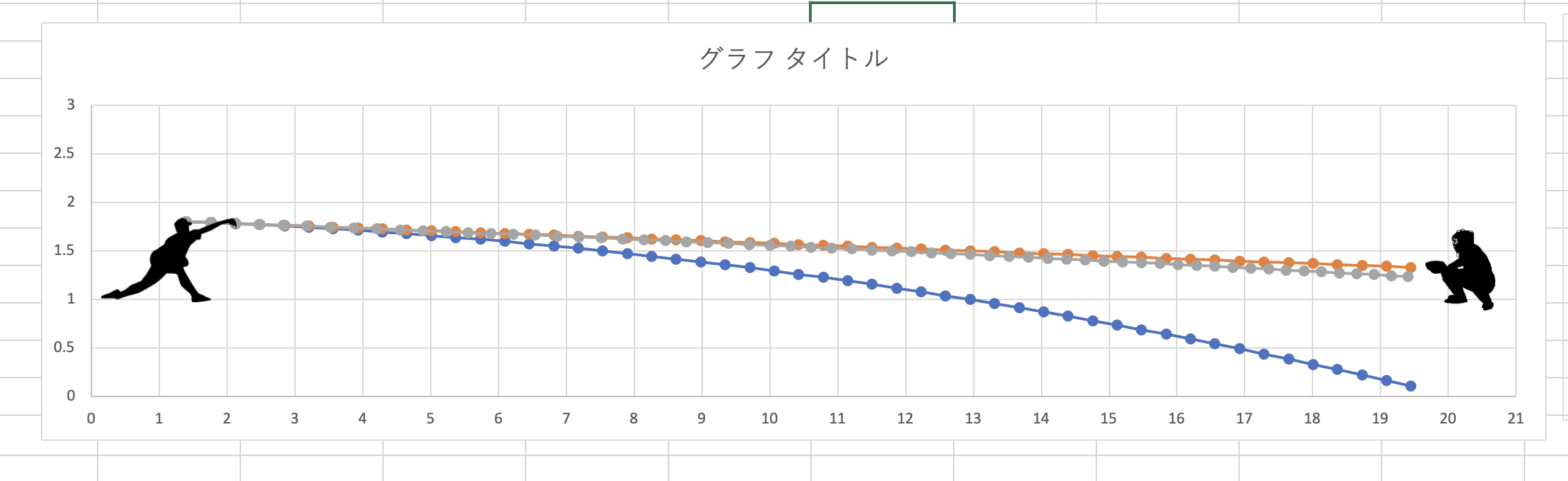
できました!
空気抵抗レベルの変化なのでそこまで大きな変化がなく、わかりにくいと思いますが
実は今回のグラフ(灰色)は最大時間を 0.5s から 0.6s にしています。
しっかり抗力がかかって、0.5s ではキャッチャーまで届きませんでした。
追記:2023/08/11
すみませんっ!
これでは重力が実装されていませんね。

上記画像が正しい計算式です。
重力(-0.5$C$9L3*L3)を追加するだけです。
=$C$4+$C$6SIN(RADIANS($C$7))L3-0.5$C$9L3*L3
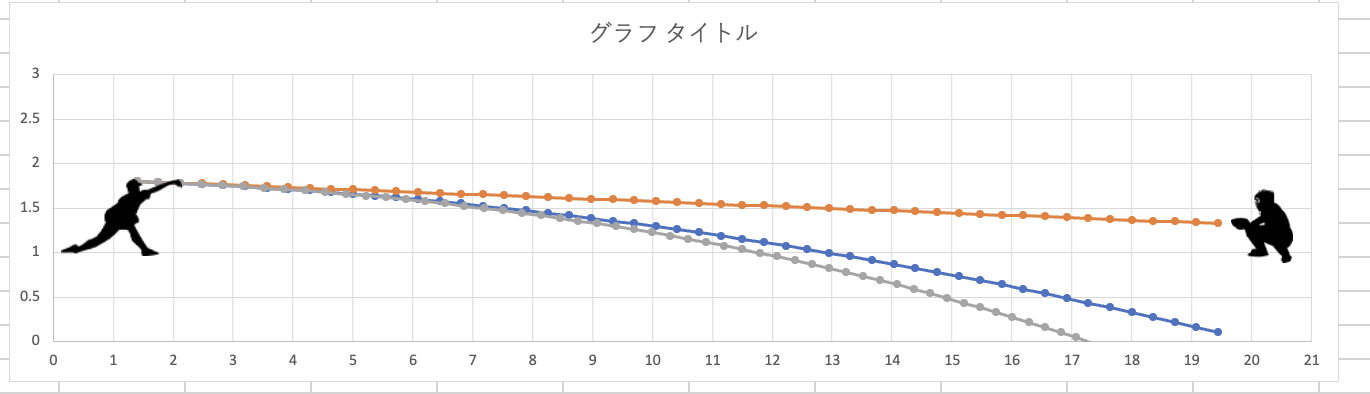
これで揚力以外実装できました!
全然違いますね笑
ほんと、すみません。
最後に
今回までで、ボールにかかる力上下前後のうち、上以外にかかる力を全て実装しました。
本当は今回の記事で全て実装するつもりでしたが、空気抵抗の計算が想像以上に大変で時間がかかってしまいました。
なので、次でやっと完成です。
時間がかかってすみません。
ではまた。















コメント