今回も前回に続きExcelを使った野球の投球軌道シミュレーションをしていこうと思います。

↓ 毎度お世話になっている参考サイトさん
これまでの実装内容
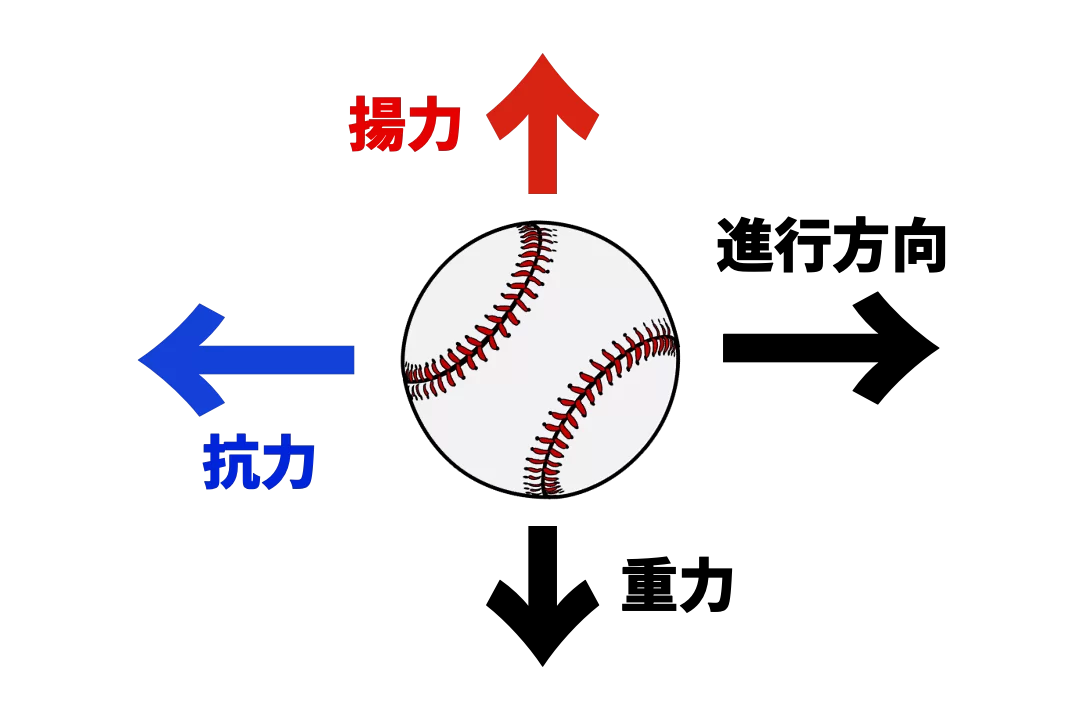
まず投球にかかる力や物理の基本的な話を勉強して

揚力以外の進行方向の力・重力・抗力をExcelでシミュレーションできるよう実装しました。
ということで、今回は残りの上にかかる力「揚力」を計算して実装していきます。
第6回 軌道シミュレータver.3.1 -揚力-
今回も参考記事に従って作っていきます。
今回参考にする記事 第6回 軌道シミュレータver.3.1 -揚力-
はじめに

今回は揚力という上向きの力を計算していきます。
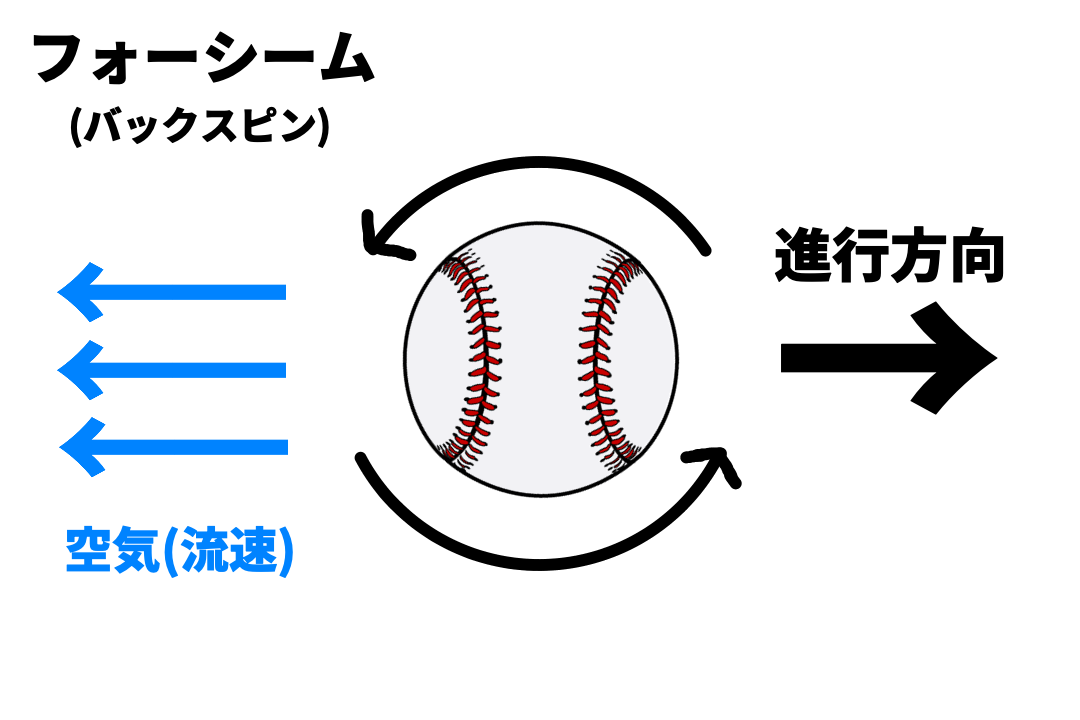
揚力にはマグヌス効果というボールの回転数が関わってきます。
藤川球児のストレートは火の玉ストレートと呼ばれ、ボールが上がるように見えると言われているのは
この回転数が高く回転の軸がほぼまっすぐだからです。
回転数が高いとこの揚力が大きくなり、本来重力により落ちてくるはずのボールが落ちづらくなるので
目の錯覚でボールが上がってくるように見えるというわけです。
計算方法について
揚力も空気抵抗の一部なので以下のように、前回の抗力と似たような形で計算できます。
L = CL × ( 0.5 × ρ × v2 ) × A
(CL:揚力係数 ρ:空気密度 v:速度 A:断面積)
抗力係数が揚力係数に置き換わっただけです。
ボール回転軸をθs, ボールのジャイロ成分をφsとします。
θ = 90° を真っ直ぐな綺麗な回転として、今回は θ = 100°とします。
ジャイロ成分は φs = -80° とします。
X座標の計算式は前回同様です。
抗力 :D = CD × ( 0.5 × ρ × v2 ) × A
加速度:d2x/dt2 = -CD × ( 0.5 × ρ × (dx/dt)2 ) × A / m
速度. :dx/dt = ∮(d2x/dt2)dt
位置. :x = ∮(dx/dt)dt
速度. :dx/dt = v0 × cosθ × cosφ
位置. :x = x0
Y座標の計算式
角度によっては揚力は斜めになったりします。
斜めへのベクトル力はY軸とZ軸に分けられます。
Y軸が cos Z軸が sin 。
ということで、Y座標に揚力を計算していきます。
ただ、空気抵抗と何ら変わりないので基本的には前回・今回のX座標の計算式とほぼ同じです。
抗力 :Ly = CL × ( 0.5 × ρ × vx2 ) × A × cosθs
加速度:d2y/dt2 = CL × ( 0.5 × ρ × (dx/dt)2 ) × A × cosθs / m
速度. :dy/dt = ∮(d2y/dt2)dt
位置. :y = ∮(dy/dt)dt
速度. :dy/dt = v0 × cosθ × sinφ
位置. :y = y0
Z座標の計算式
Z座標の計算式も、Y座標の計算式同様ですが、重力加速度を追加します。
抗力 :Lz = -CL × ( 0.5 × ρ × vx2 ) × A × sinθs × sinφs
加速度:d2z/dt2 = -CL × ( 0.5 × ρ × (dx/dt)2 ) × A × sinθs × sinφs / m – g
速度. :dz/dt = ∮(d2z/dt2)dt
位置. :z = ∮(dz/dt)dt
速度. :dz/dt = v0 × sinθ
位置. :z = z0
x0, y0, z0:リリース位置 v0:リリース時の球速
θ:上向きリリース角度 φ:横向きリリース角度
t:リリース後経過時間 g:重力加速度
実際にExcelでシミュレーションしてみる
では実際にExcelに入力していきます。
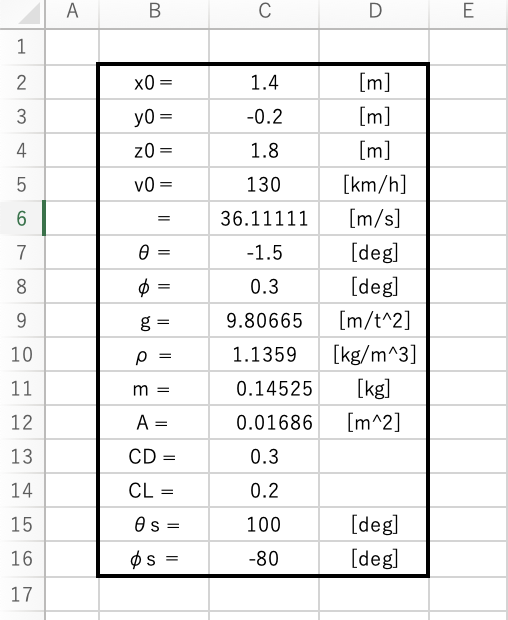
上記のように定数をまず設定しました。
これまでに引き続き、今回は CL, θs, φs を定数として新たに設定します。
CL:揚力係数は、抗力係数と同様に求めることが、かなり難しく(実際に実験や計算をしないといけない)
また回転数によっても変化しますが、野球ボールに関する先行研究をいくつか調べてみたところ
回転数が毎分2500回のとき約0.2 ということがわかりました。
ということで、今回は 0.2 として計算します。
ちなみに毎分2500回というのは、大谷翔平でも平均2200回、シーズン中1番調子が良い時で2600回越えなので
かなり高い回転数になっています。
以下、前回と同様のX座標の計算式
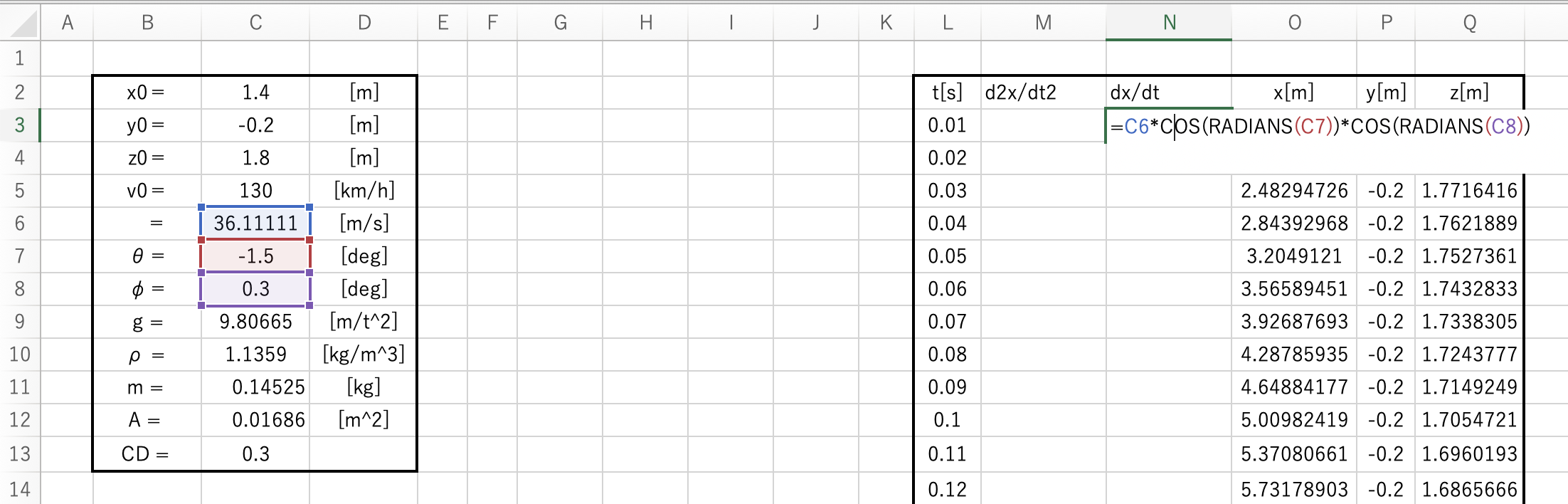
先ほどの t = 0 のときの速度計算式を入力。
=C6COS(RADIANS(C7))COS(RADIANS(C8))
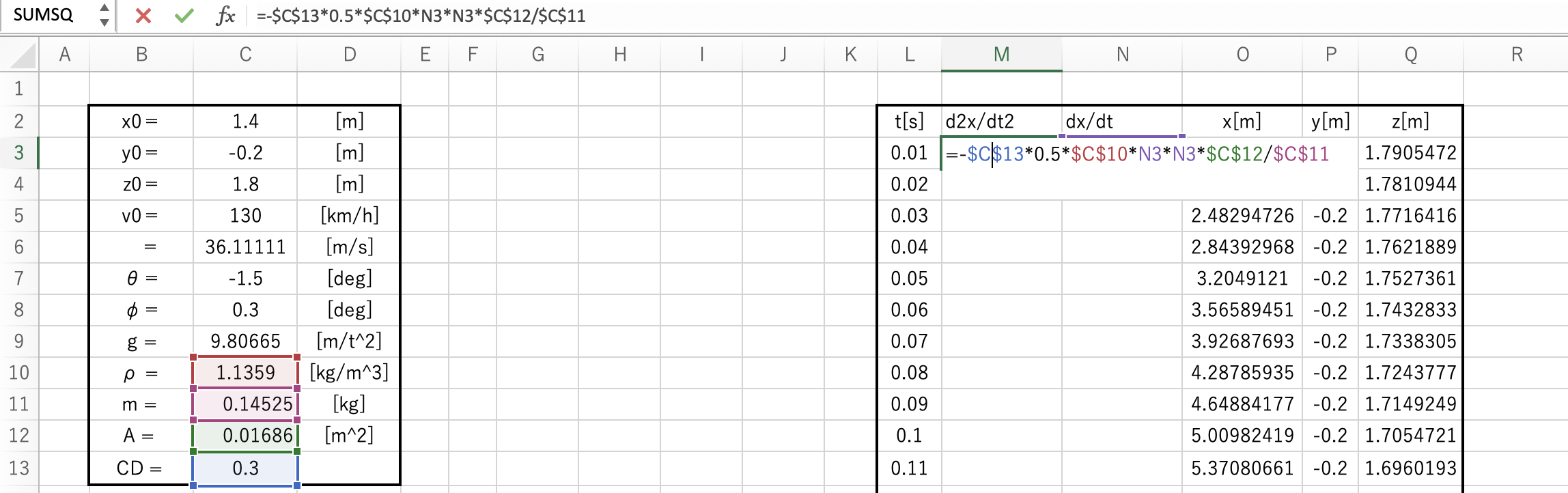
次に加速度を先ほどの計算式を入力していきます。
=-$C$130.5$C$10N3N3*$C$12/$C$11

また、今度は t = 0ではないときの通常の速度を求める計算式を入力していきます。
ただ、速度を求めるには積分をするのですが、積分を分解して普通に計算していきます。

あっすみません、t が 0 からじゃなかったので修正しました。
0.01 だったセルを 0 に変えるだけで全部自動で値が変わるのでExcelは便利ですね ^^;
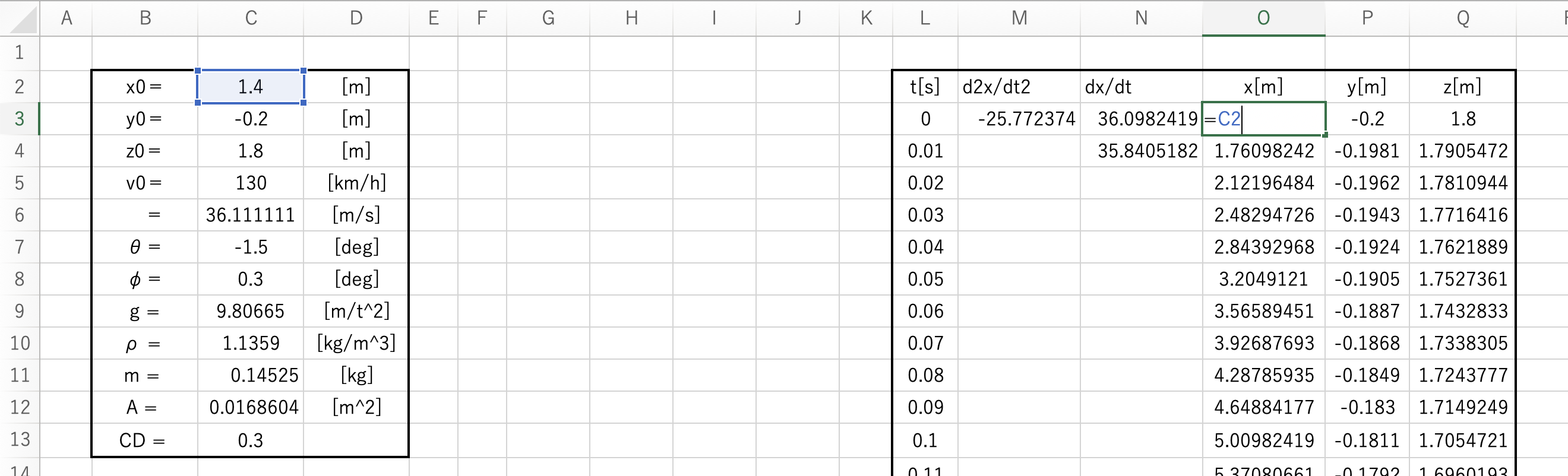
t = 0 のときの位置の計算式を入力します。
といってもリリースポイントの初期値そのまま渡すだけですが笑
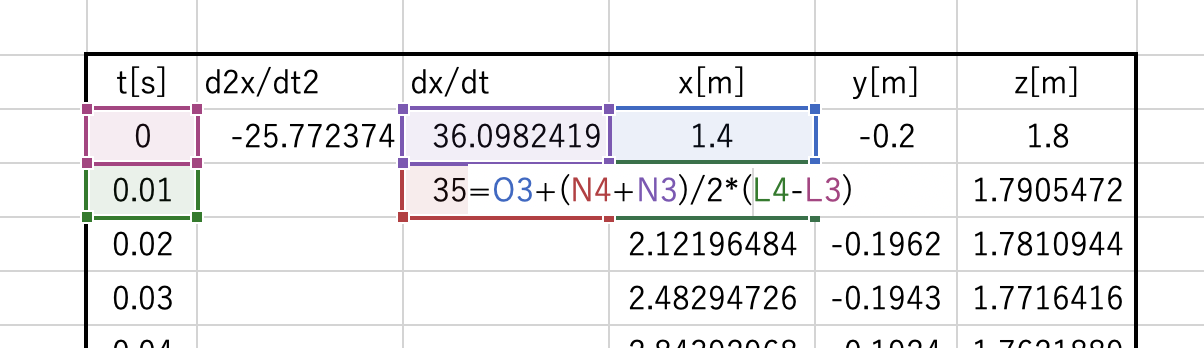
また、今度は t = 0ではないときの通常の速度を求める計算式を入力していきます。
ただ、こちらも速度同様、位置を求めるには積分をするのですが、積分を分解して普通に計算していきます。
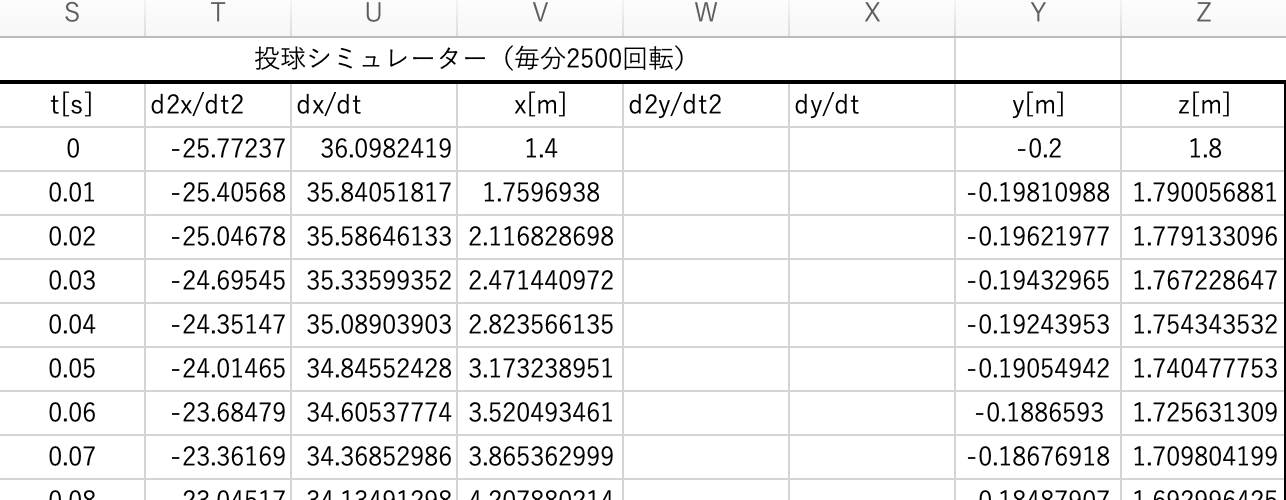
前回のX座標と同様に d2y/dt2 と dy/dt の列を追加します。
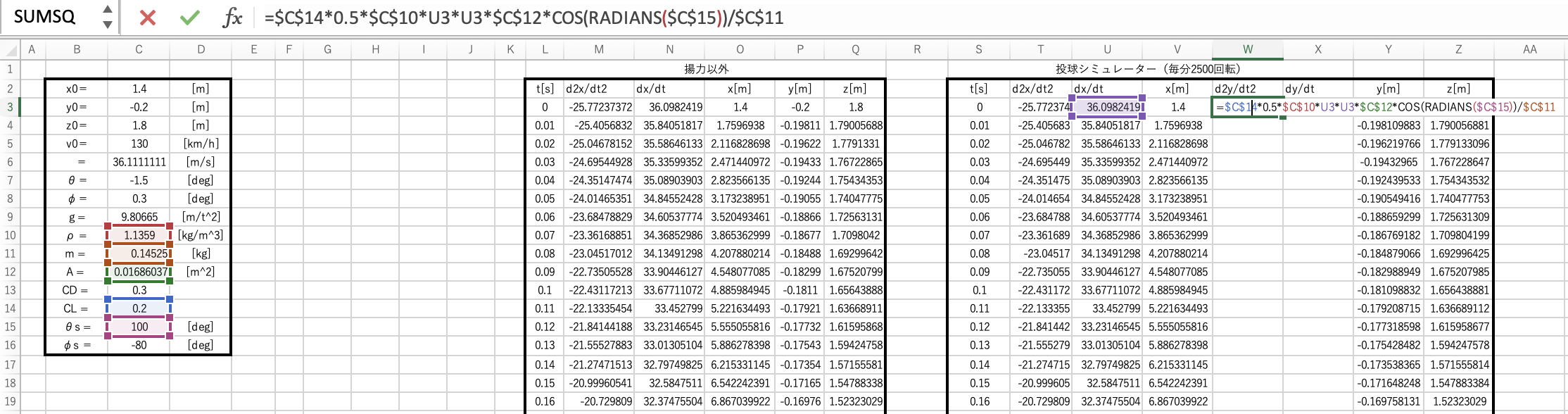
先ほどのY軸の加速度の計算式 d2y/dt2 = CL × ( 0.5 × ρ × (dx/dt)2 ) × A × cosθs / m を使い
d2y/dt2 を計算していきます。
=$C$140.5$C$10U3U3$C$12COS(RADIANS($C$15))/$C$11

t = 0 の時の速度の欄に dy/dt = v0 × cosθ × sinφ を使い
dy/dt を計算していきます。
画像では定数が$で固定されてませんが、固定しておいてください。
=$C$6COS(RADIANS($C$7))SIN(RADIANS($C$8))
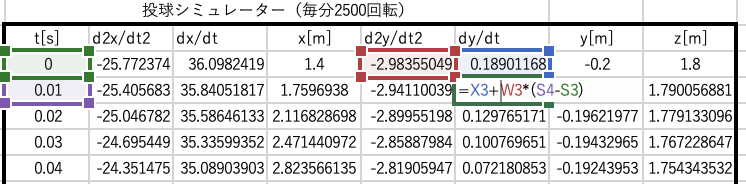
今度は t > 0の時の速度を dy/dt = ∮(d2y/dt2)dt を使い求めるのですが
積分は分解して普通に計算していきます。
=X3+W3*(S4-S3)

t = 0 の時の位置の欄に y = y0 を使い、位置を計算していきます。
計算といっても代入するだけですが笑

今度は t > 0の時の速度を y = ∮(dy/dt)dt を使い求めるのですが
こちらも積分は分解して普通に計算していきます。

ん?
明らかにシュートしすぎですね


調べてみると参考記事とボールの断面積が大きく異なっていました。
誤差なんと約0.013も!?
う〜ん、、、
分かりました!完全な私の計算間違いです。
半径ではなく直径を使っていました笑

無事、正しい軌道が再現できました。
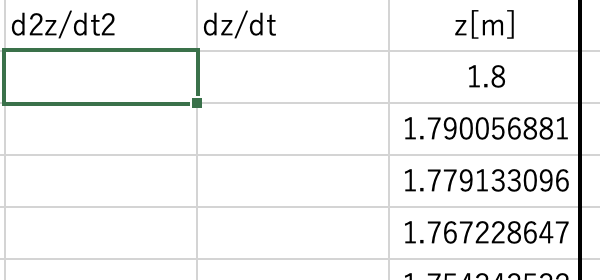
Y座標と同様に d2z/dt2 と dz/dt の列を追加します。

先ほどのZ軸の加速度の計算式 d2z/dt2 = -CL × ( 0.5 × ρ × (dx/dt)2 ) × A × sinθs × sinφs / m – g を使い
d2z/dt2 を計算していきます。
=-$C$140.5$C$10U3U3$C$12SIN(RADIANS($C$15))*SIN(RADIANS($C$16))/$C$11-$C$9

t = 0 の時の速度の欄に dz/dt = v0 × sinθ を使い
dz/dt を計算していきます。

今度は t > 0の時の速度を dz/dt = ∮(d2z/dt2)dt を使い求めるのですが
こちらも積分は分解して普通に計算していきます。
=AA3+Z3*(S4-S3)
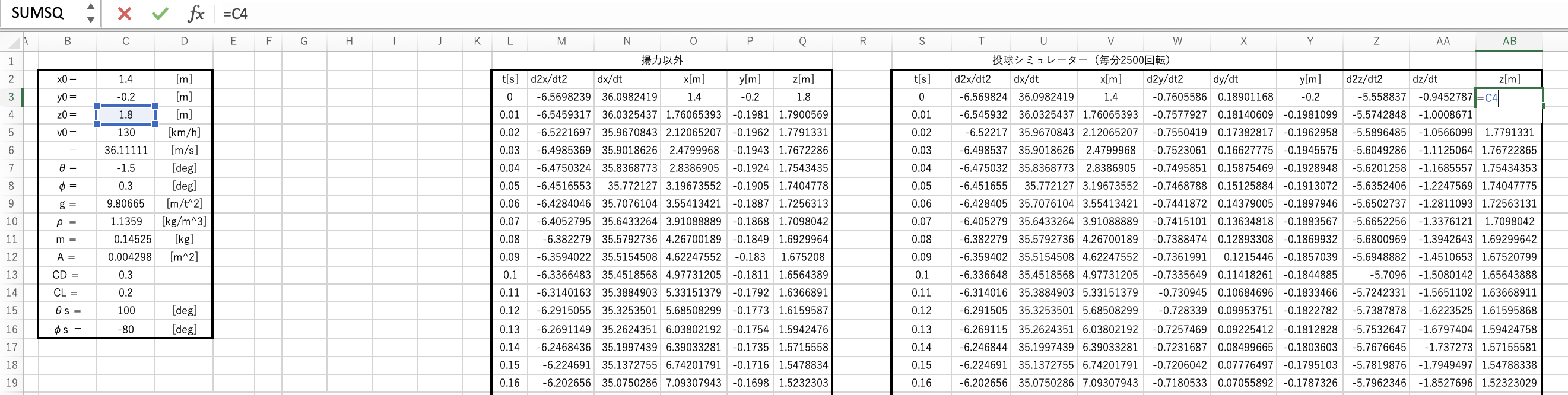
t = 0 の時の位置の欄に z = z0 を使い、位置を計算していきます。
Y軸のとき同様、計算といっても代入するだけです笑
=$C$4

今度は t > 0の時の速度を z = ∮(dz/dt)dt を使い求めるのですが
こちらも積分は分解して普通に計算していきます。
=AB3+AA3*(S4-S3)
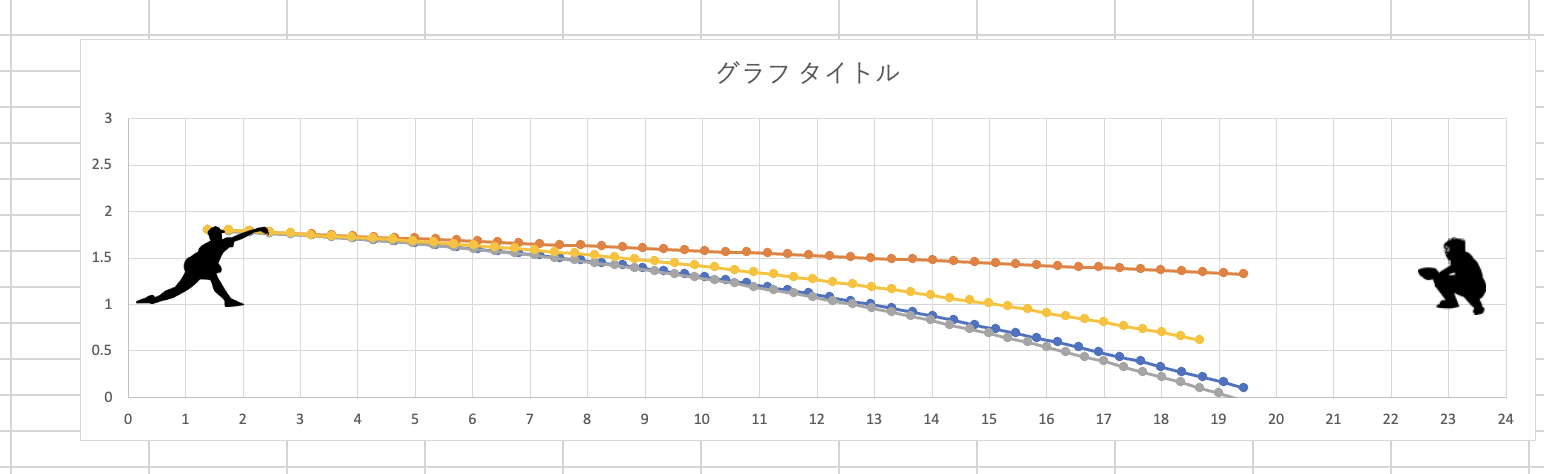
完成しました!!
いや〜結構ここまで時間かかりましたね!
黄色のグラフが今回実装した毎分2500回転するストレートの軌道になります。
最後に
今回はここまでです!
多分ですが次は回転数による変化をシミュレーションすると思います。
もう少しお付き合いよろしくお願いします。
ではまた。














コメント