こんにちは、前回リアル野球ゲームを作ると言いました。

ただ、調べてみるとUnityには現実に即した正確な物理演算ができないみたい、、、
なので今回は投球に関する物理について学び理解していこうと思います。
面白いサイト見つけた!
野球の投球について調べていると、こんなサイトを見つけました。
このサイトでは上記のようにExcelを使い、投球シミュレーションをしています。
これが再現できたら3DのUnity上でも再現できるのでは?
と思ったので今回はこのExcelを使った投球起動シミュレーションを作ってみようと思います!
ちなみに、とても親切なサイトで作り方まで公開してくれています。
筆者の開発環境

PC: MacBookAir M1チップ 2020年モデル
Excel: Microsoft 365
多分ですが、高度な計算や莫大な計算量ではないので
Excelが動かせる環境なら古いノートPCでも何でも大丈夫だと思います。
第1回 等速直線運動の再現
はじめに
今回はまずサイトの記事通りに作ってみようと思います。
今回参考にする記事 第1回 軌道シミュレータver.1 -等速直線運動-
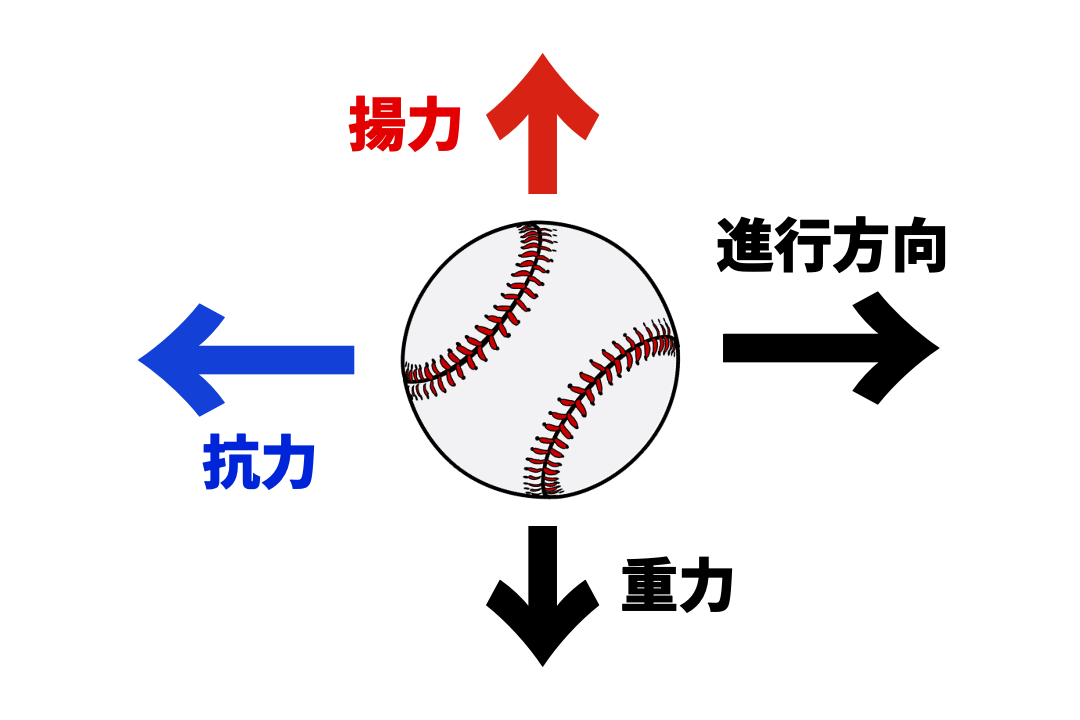
第一回ではまず重力と空気を完全に無視した条件で計算するようです。
上記のように投げたボールには前後上下にそれぞれ物理的な力が加わります。
そのため一つずつ力を再現(計算)していこうと言うことでしょう。
このような、現実世界の物理的な力を全て計算するのではなく、
簡略化し一部だけを計算することを物理学では「理想化」というそうです。
高校で習う物理の問題もこんな感じで空気抵抗などは全て無視でしたね。
「エクセルで野球ボールの軌道計算」の筆者さんは、物理に精通している方なのでしょうか。
それとも、単に私の知識不足なんですかね(笑)

さて、重力と空気を完全に無視した場合はピッチャーの投げる力しか受けないので
上記画像のように、ボールにかかる力の向きは「進行方向」のみです。
向きだけでなく、速さも一定で直線の動きをします。
これが、みなさんご存知「等速直線運動」です。
それでは実際に計算していきます。
計算方法について
計算式も「エクセルで野球ボールの軌道計算」のサイトに載っているものをそのまま使わさせて頂きます。
ただ、そのまま使うだけでは勉強の意味がないので、しっかり理解していきます。
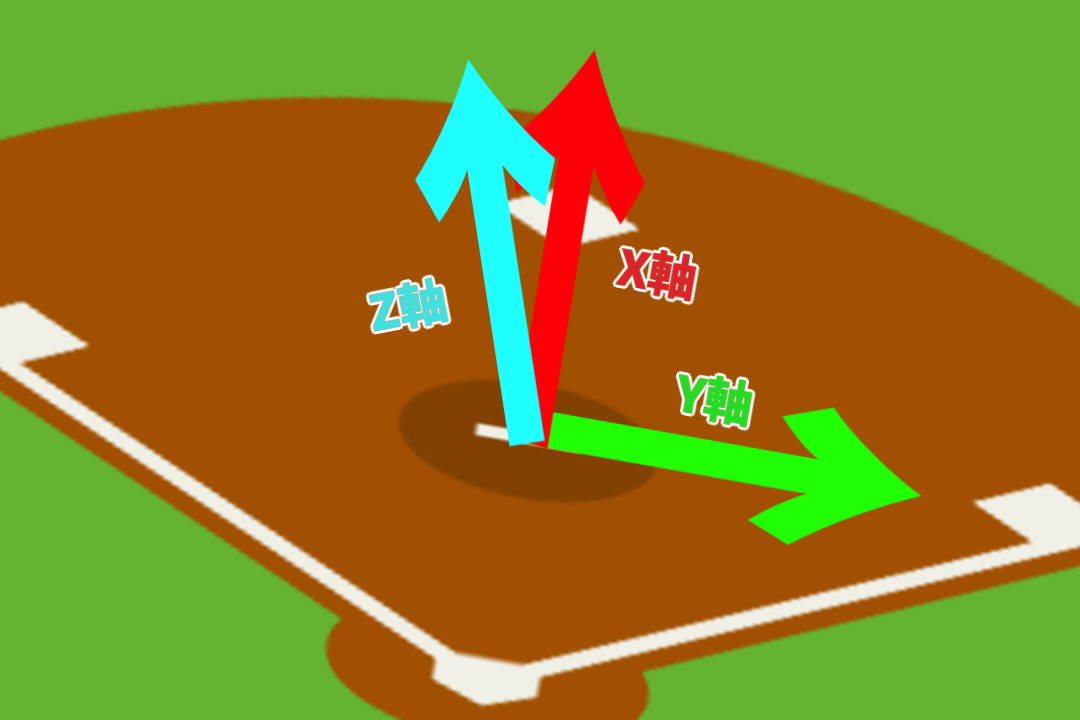
ピッチャーから見て x軸を前後方向 y軸を左右方向 z軸を上下方向
一応画像にしてみました。わかりにくかったらゴメンなさい。
計算式は以下のようです。
x = x0 + v0 × cosθ × cosφ × t
y = y0 + v0 × cosθ × sinφ × t
z = z0 + v0 × sinθ × t
x0, y0, z0:リリース位置 v0:リリース時の球速
θ:上向きリリース角度 φ:横向きリリース角度
t:リリース後経過時間
単位系はSI単位系という単位系を使うようで
距離が キロメートル(km)→ メートル(m)
時間は 時間(h)→ 秒(s)
そのため、球速は時速(km/h)→ 秒速(m/s)を使用されてます。
以下、各計算式の解説
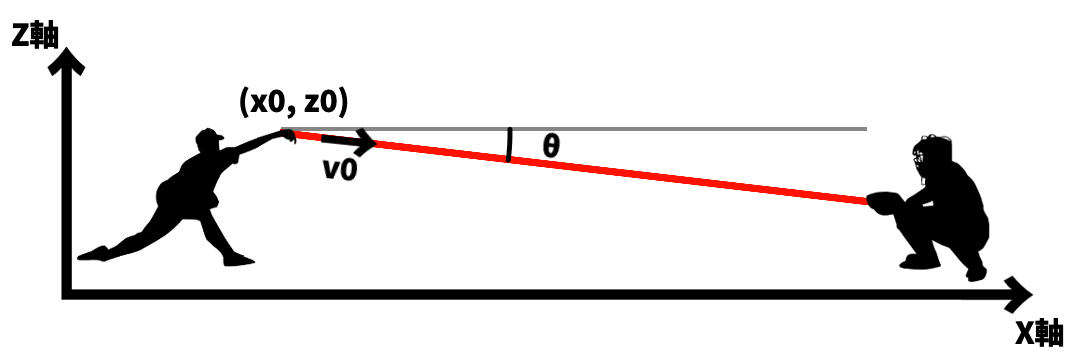
上記はY軸方向から見た画像です。
x = x0 + v0 × cosθ × cosφ × t
cosθ をかける理由は、
cos0° = 1, cos90° = 0 のように cos をかけることで角度による座標の変化を計算できるからです。
cosφも同様の考え方です。
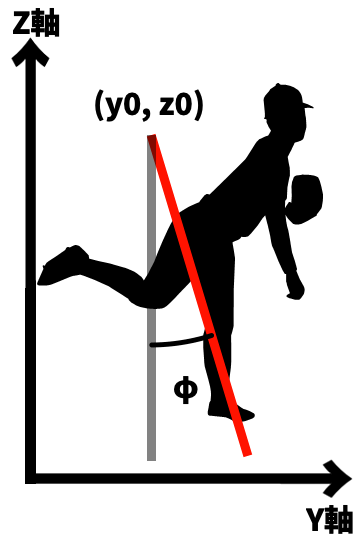
y = y0 + v0 × cosθ × sinφ × t
cosφ ではなく sinφ をかける理由は、
φ が 0° のときY座標は変化しません。
sin0° = 0 となるので、cosφ ではなく sinφ をかけます。
cosθ は先ほどのX座標の考え方と同様です。


z = z0 + v0 × sinθ × t
z座標の計算式だけは少し異なり、cos や sin は sinθ 1つだけで φ はありません。
上記の図を見て貰えばよくわかると思いますが、Z座標の計算に φ は必要ありません。
cos ではなく sin を使う理由は、θ が 0° のときZ座標は変化しないので、cos0° = 1 ではいけません。
sin を使うことで、sin0 = 0, sin45 = 0.5, sin90 = 1 となるので座標を正しく計算できます。
実際にExcelでシミュレーションしてみる
やっと本題のExcelを使った等速直線運動のシミュレーションです。
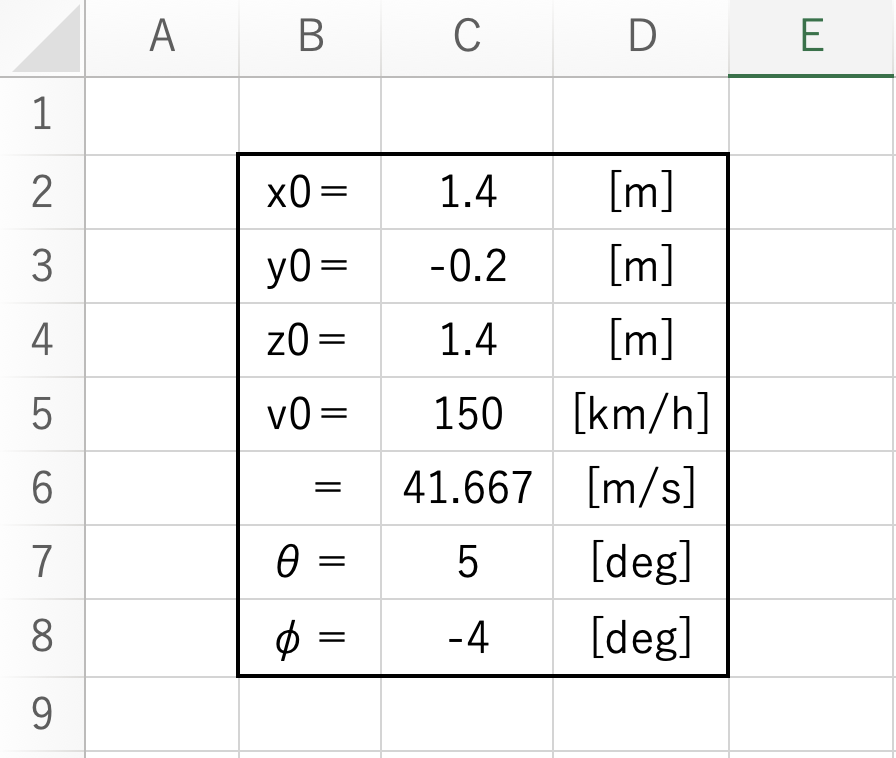
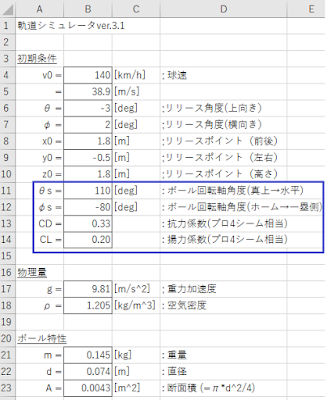
まず上記のように、数式で使う変数を全て用意します。
今回は右投げオーバースローで数値を考えてみました。
km/h → m/s の変換は時速を 3.6 で割るだけでOKです!
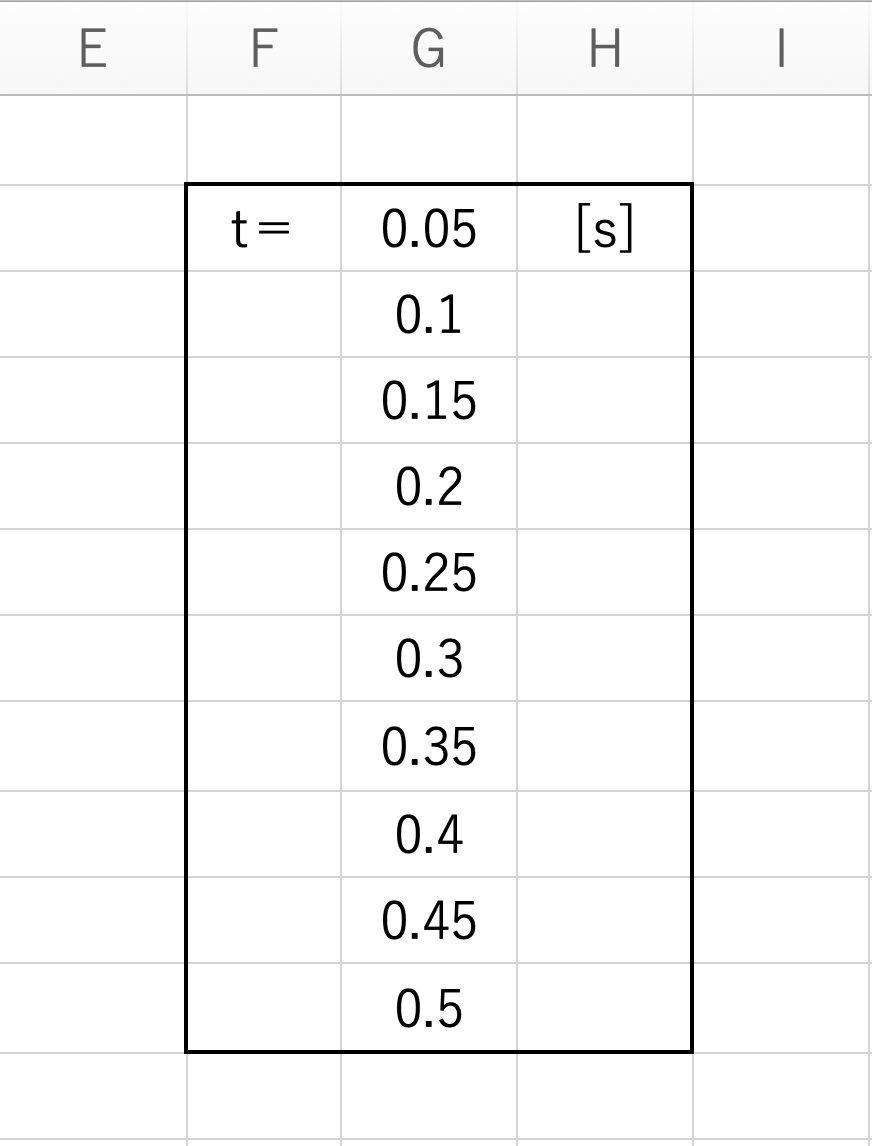
次に時間経過で投球軌道の点をプロットするために t を複数用意しました。
今回、私は 0.05[s] ごとにプロットするようにしましたが、参考記事では 0.02[s] なので自由に決めてOKです。
Unityでは描画間隔の値がこれになりそうですね!
ちなみにプロ野球のリリースからキャッチャーに届くまでの時間は 0.4~0.5 なので、最大を 0.5 と設定しました。

次にそれぞれの座標を求める計算式を入力していきます。
上記はX座標の計算式です。
角度が deg なので計算式で扱えるよう radian に変換します。
RADIANS(θ) または θ*PI()/180 で radian に変換できます。
t のセル以外の定数は全て $ か F4 で固定してください。
=$C$2+$C$6COS(RADIANS($C$7))COS(RADIANS($C$8))*I3
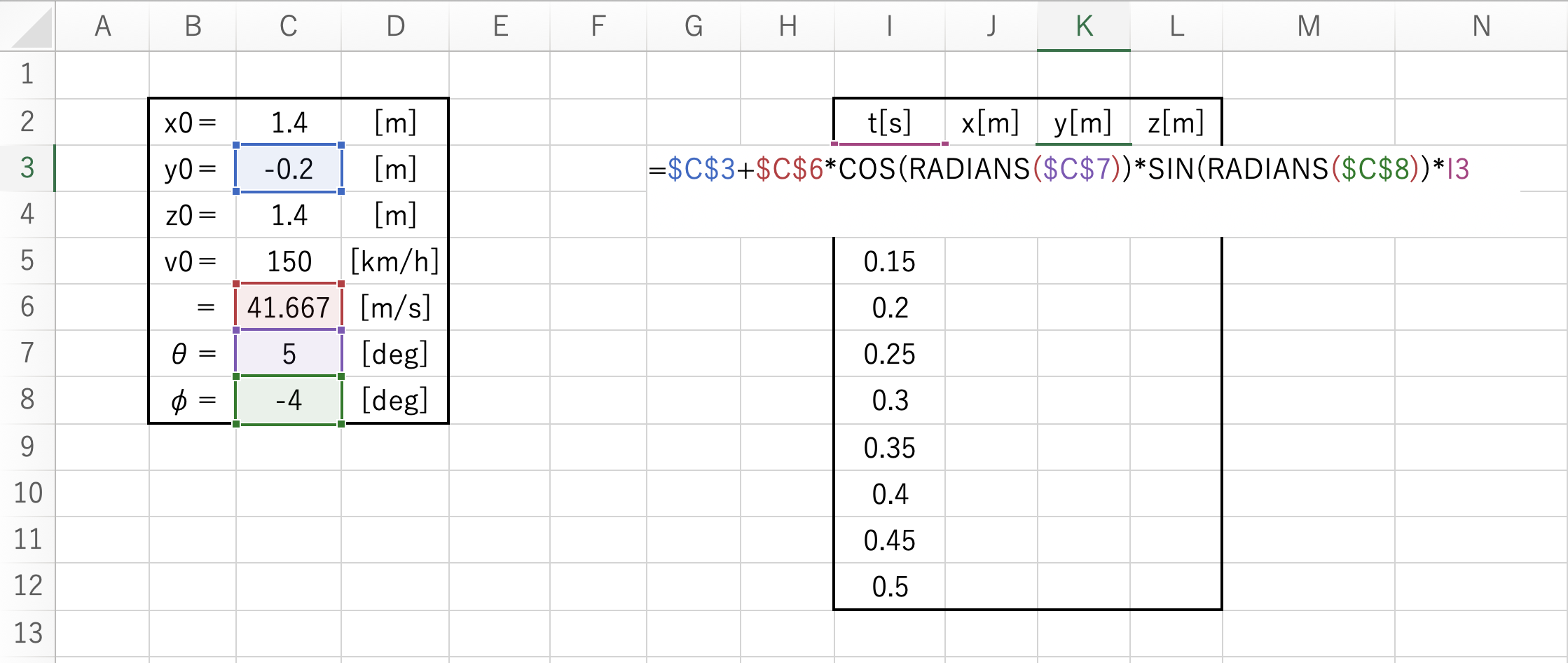
上記はY座標の計算式です。
=$C$3+$C$6COS(RADIANS($C$7))SIN(RADIANS($C$8))*I3
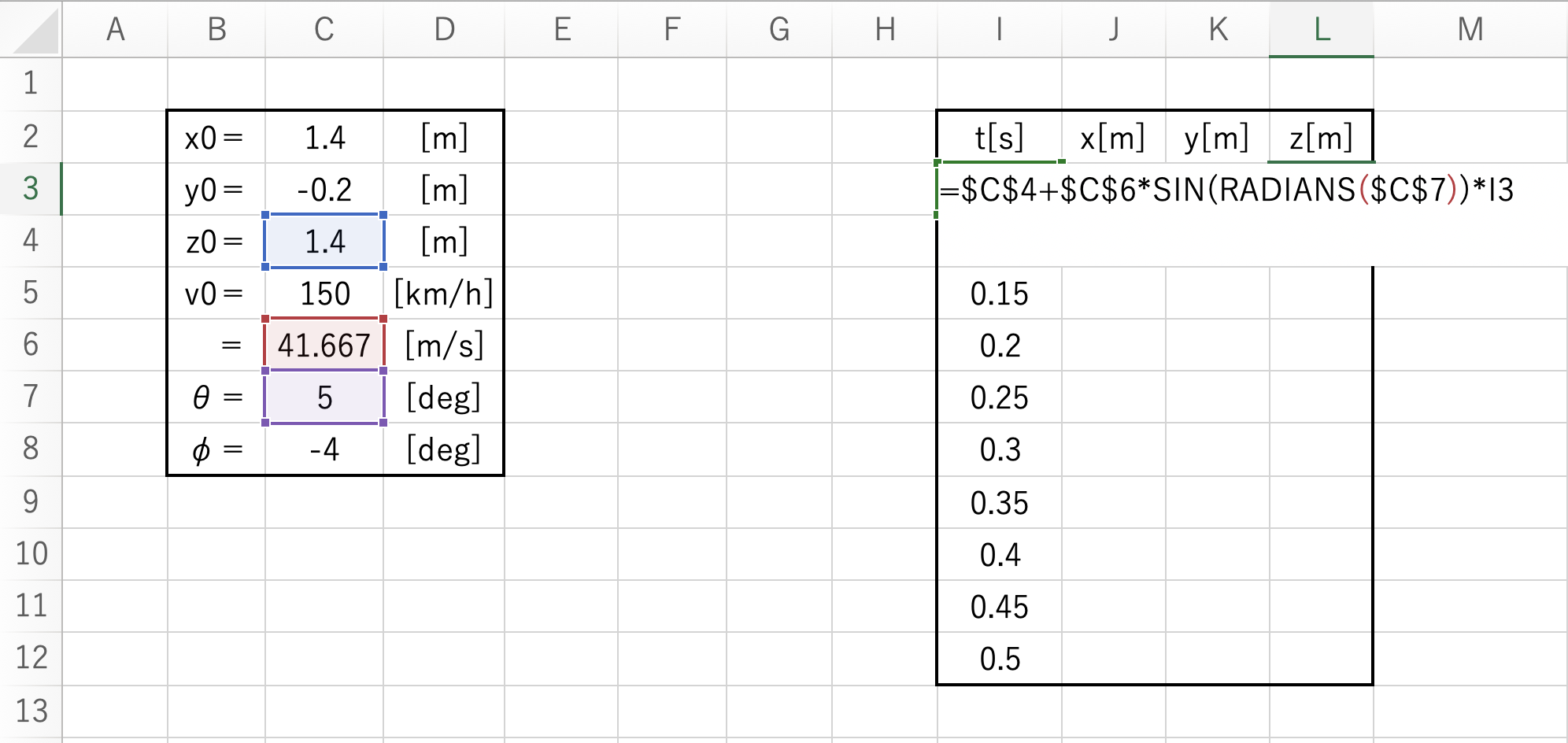
上記はZ座標の計算式です。
=$C$4+$C$6SIN(RADIANS($C$7))I3
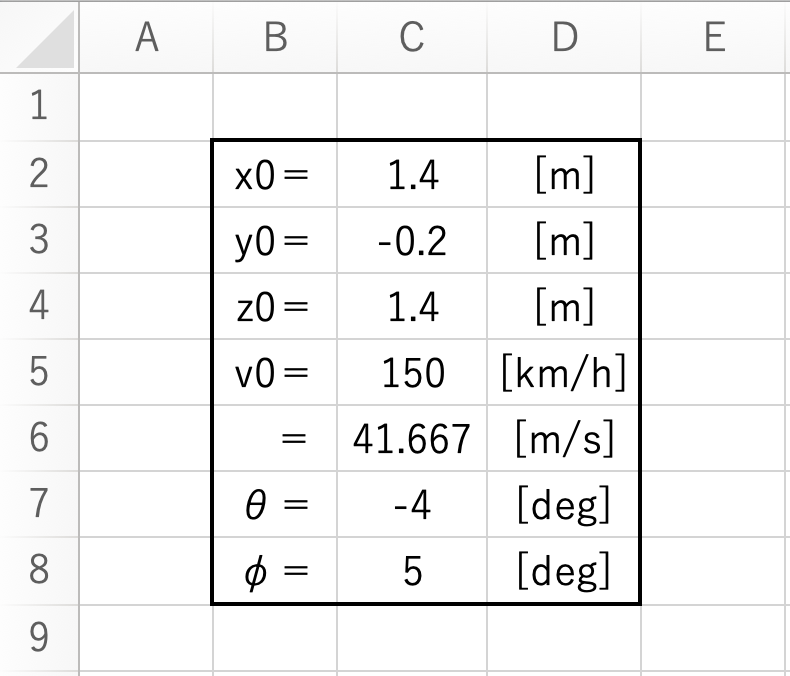
あっ、すみません〜
θ と φ の値を逆にしてください!
これだと上に飛んでいってしまいますね💦
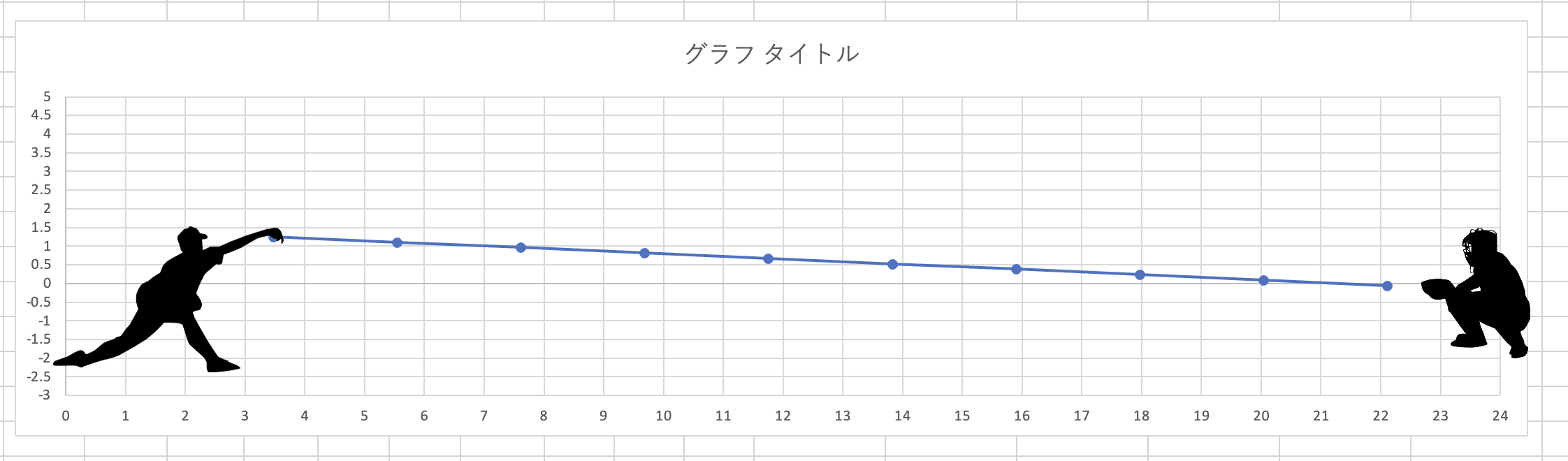
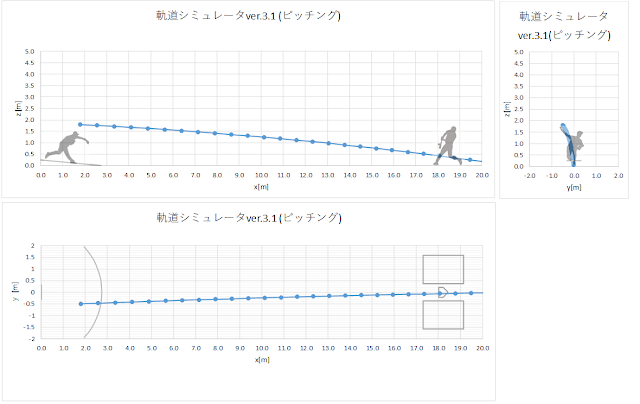
できました!
ただ、Z軸がマイナスになってしまったので、人間は地面に埋まりました(笑)
θ がデカすぎましたね、、、しかし等速直線運動の軌道自体は上手できているように見えますね!!
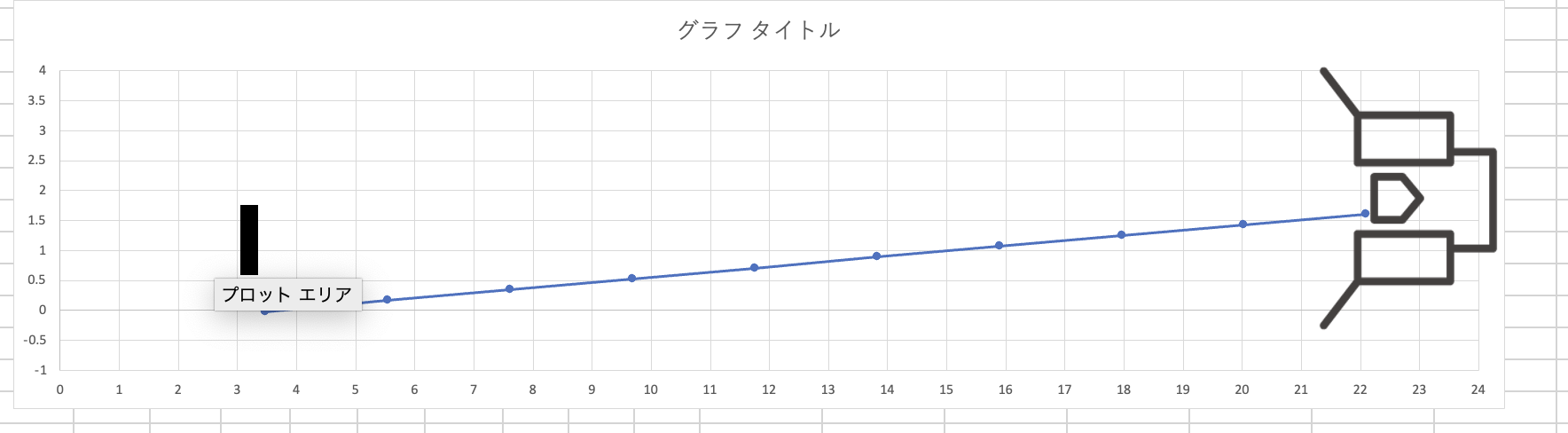
上からもうまく出来てますね!
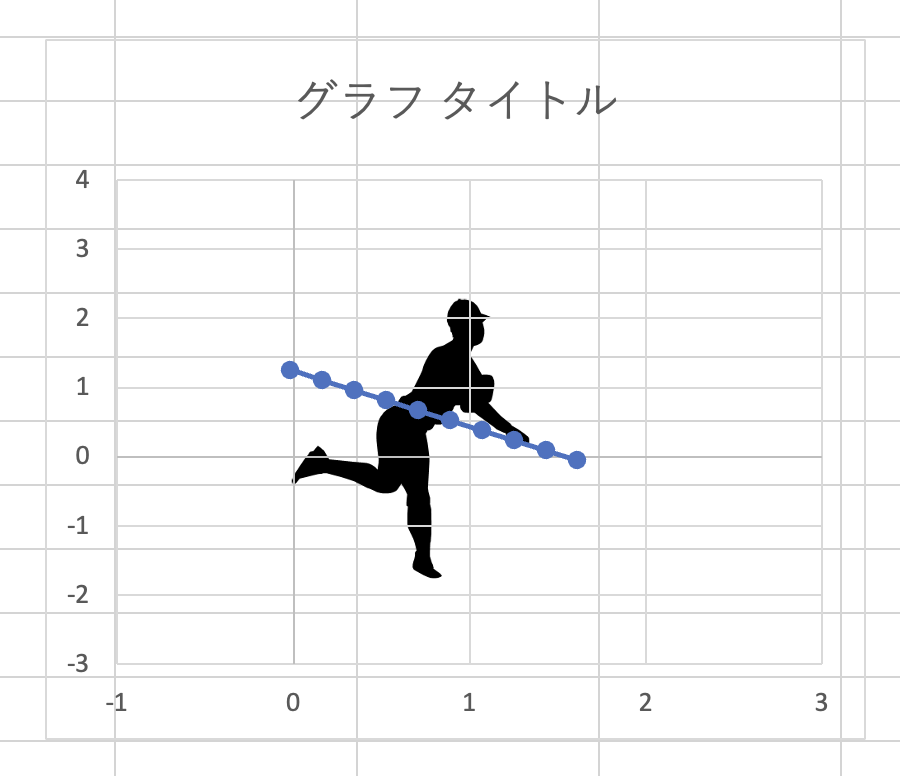
相変わらず角度はムチャクチャですが、キャッチャー目線もしっかり出来てるみたいです。
めっちゃサイド軌道ですね笑
さいごに
今回久しぶりのExcelでグラフの作り方すら、まともに分からなかったので時間がかかりすぎてしまいました。
いや〜疲れました笑
ほんとは参考サイトの記事を複数まとめて1記事で、実装していこうと思ったのですが
想像以上に時間と文字数がかかってしまったので、今回は「第1回 等速直線運動の再現」だけで終わりにします。
次はもっと1記事でもっと進めていこうと思います。
それではまた。
















コメント